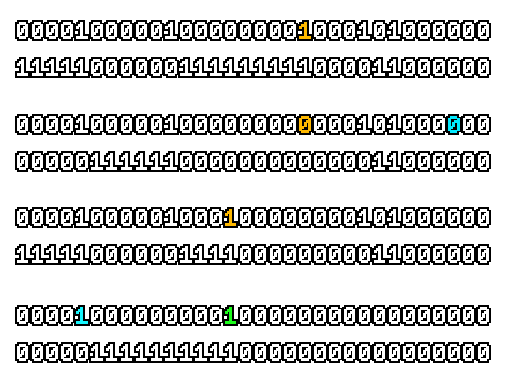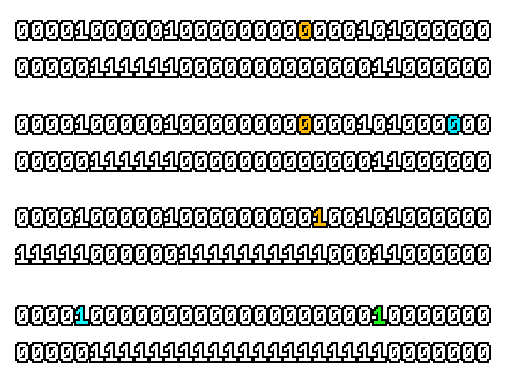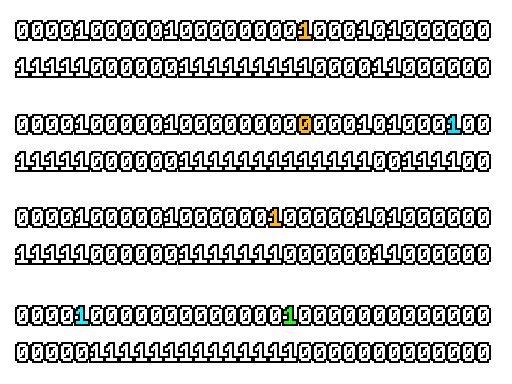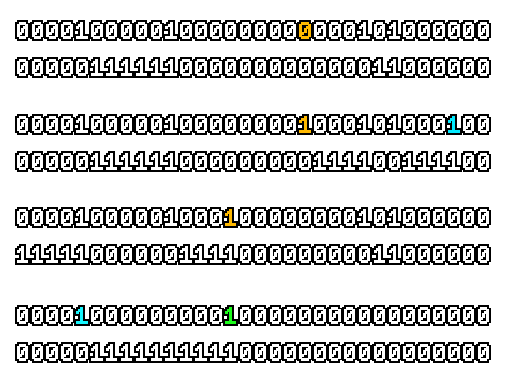
Carry-less products find their natural habitat in finite field arithmetic, common in error checking codes and in encryption and checksums.
Finite field arithmetic(aka Galois Fields) is very different from the usual addition and multiplication rules that you know, especially GF(2)(Binary Galois fields) which are very easy to implement with pre-existing binary computers.
Galois(pronounced gal-wah) fields are named after Évariste Galois. A very young French activist that was also a very talented mathematician that died at the young age of 20 due to a duel.
It’s gonna be hard to pretend like I know everything about GF(2) finite fields but basically it’s a number system where every element is the set of numbers within modulo-2(a number system of just two numbers, 0 and 1) and where addition/subtraction, multiplication, and division operations are closed(well defined) within the set of numbers. GF(2) is a fully satisfied finite field that defines all of these operations but we’ll just explore addition and multiplication here. A single 0 or 1 bit is a single GF(2) number. A 16/32/64 bit integer may be interpreted as a compact vector of 16/32/64 GF(2) numbers. A vector of GF(2) numbers bundled together may also represent a large 16/32/64/n-degree polynomial of GF(2) numbers, also known as GF(2n).
GF(2n) is where each bit[i] corresponds to a binary 0/1 coefficient of the xi-th polynomial term.
So, a uint64_t(64-bit integer) has the potential of being a 63-degree polynomial within GF(2^64):
bit[0] * x0 + bit[1] * x1 + bit[2] * x2 + … + bit[63] * x63
Addition
Adding polynomials in the general case is simply adding similar terms(if they share the same base and exponent, add their coefficients)
(xa + xb + xc) + (xa + xc) = 2xa + xb + 2xc
But! This is GF(2), so we have to modulo-2 the coefficients for each of these exponents to make this polynomial representable in GF(2). Causing “2xa” and “2xc” to disappear(2 % 2 = 0);
(xa + xb + xc) + (xa + xc) = 2xa + xb + 2xc —(mod2)—> xb
The binary representation of this addition shows that it is equvilent to the binary exclusive-or(XOR) operator(^ in C++). XOR is a simple boolean operation that returns 1 if the two inputs bits are different.
This is the same as the logical “not equal” operator in many languages(!=) or can be thought of as parity(if the number of 1 bits is odd(1) or even(0)). It can also be thought of as an addition where we ignore the carry. So when we add 1 + 1, we return 0, but we don’t propagate a 1 into the next digit:
(x2 + x1 + x0) + (x2 + x0) = x1
“111” + “101” = “010”
111 ^ 101 = 010
Multiplication
Multiplying polynomials in GF(2n) almost the same as multiplying regular polynomials(distribute and multiply terms, and then add together like-terms of the same base and exponent into an increased coefficient), except there is still a n % 2 reduction to the coefficients to keep them within GF(2) causing some terms to disappear.
As a simple case, lets multiply a general polynomial by a single x term:
(xa + xb + xc) * x = xa + 1 + xb + 1 + xc + 1
(xa + xb + xc) * x4 = xa + 4 + xb + 4 + xc + 4
(xa + xb + xc) * xn = xa + n + xb + n + xc + n
All this does is add n to the exponent of each term with the same base! Just a little refresher on the product-law of exponents(xa * xb = xa + b).
When we observe the bit-representation GF(2n) polynomials, this is the same as a bitshift to the left by n.
(x3 + x1) * x = x3 + 1 + x1 + 1 = x4 + x2
“1010” * “0010” = “10100”
1010 « 1 = 10100
(x3 + x1) * x4 = x3 + 4 + x1 + 4 = x7 + x5
“1010” * “10000” = “10100000”
1010 « 4 = 10100000
So if we wanted to multiply two binary-polynomials: Distribute-multiply each of the terms of one operand into the other separately like we just did for our single-term case(which is just a bit-shift by the bit-index of each 1 bit), and then add(XOR) all the terms together!
Carryless multiply: 0110 * 1010
(“0110” * “1000”) + (“0110” * “0010”)
(“0110” « 3) + (“0110” « 1)
“0110000” + “01100”
0110000 ^ 01100
111100
This works a lot like binary long-multiplication, but ignoring the carry when we add up the intermediate terms… A carry-less multiplication
1 0 1 0 = a
0 1 1 0 = b
1) "for each set bit in `a`, make a version of `b` that is bit-shifted to the left by the index of the set bit, shifting in zeros"
1 0 1 0
^ ^
| |
| +-> "0010" : bit-position 1, shift `b` by 1
+-----> "1000" : bit position 3, shift `b` by 3
0 1 1 0 = b
----------------
0 1 1 0 << 1 --> 0 1 1 0|0
0 1 1 0 << 3 --> 0 1 1 0|0 0 0
2) "Now add(xor) all of these bit-shifted terms together"
0 1 1 0 0
0 1 1 0 0 0 0
----------------
0 1 1 1 1 0 0 < Result
Here’s a more complex example with 12-bit operands. For every bit of 1 in a, we shift b to the left and xor all of these terms together.
0 0 1 1 0 1 0 1 0 1 0 1
"x" 0 1 0 0 1 0 0 0 0 1 1 1
--------------------------------------------------
0 0 1 1 0 1 0 1 0 1 0 1
0 0 1 1 0 1 0 1 0 1 0 1|0
0 0 1 1 0 1 0 1 0 1 0 1|0 0
0 0 1 1 0 1 0 1 0 1 0 1|0 0 0 0 0 0 0
"^" 0 0 1 1 0 1 0 1 0 1 0 1|0 0 0 0 0 0 0 0 0 0
--------------------------------------------------
0 0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 1 0 1 0 1 1
My technical wording is at its limit. So here’s a C++ implementation to explain it better.
#include <cstdint>
#include <cstdio>
#include <bitset>
std::uint32_t CarrylessMultiply(std::uint32_t A, std::uint32_t B)
{
std::uint64_t Result = 0;
// Iterate through all 32-bits of A
for( std::size_t i = 0; i < 32; ++i )
{
// Test the i-th bit of A
if( (A >> i) & 1 )
{
// If the bit is set, then "add"(xor) a left-shifted version of B to the result
Result ^= std::uint64_t(B) << i;
}
}
return Result;
}
int main()
{
const std::uint32_t A = 0b0110;
const std::uint32_t B = 0b1010;
std::puts(("A:\t"+std::bitset<4>(A).to_string()).c_str());
std::puts(("B:\t"+std::bitset<4>(B).to_string()).c_str());
std::puts(("A*B:\t"+std::bitset<8>(CarrylessMultiply(A, B)).to_string()).c_str());
}
// A: 0110
// B: 1010
// A*B: 00111100
Note that the result of the product needs more bits than its input operands. If polynomial a(x) has the degree of m and b(x) has the degree of n, then the result c(x) has the degree m + n
Just remember the age-old rule of multiplying exponents together of the same base that this statement is an extension of.
xm * xn = xm + n
So a 12-bit input can produce the largest polynomial x11. So a product of of 12-bit operands can potentially produce a polynomial of x22.
Lets try and make a bit-level generalization of this operation:
0 0 1 1 0 1 0 1 0 1 0 1 = a
"x" 0 1 0 0 1 0 0 0 0 1 1 1 = b
--------------------------------------------------
0 0 1 1 0 1 0 1 0 1 0 1 | 0*00*0000**1
0 0 1 1 0 1 0 1 0 1 0 1|- | 0*00*0000*1*
0 0 1 1 0 1 0 1 0 1 0 1|- - | 0*00*00001**
0 0 1 1 0 1 0 1 0 1 0 1|- - - - - - - | 0*0010000***
"^" 0 0 1 1 0 1 0 1 0 1 0 1|- - - - - - - - - - | 0100*0000***
--------------------------------------------------
0 0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 1 0 1 0 1 1 = c
^ ^ ^ ^ ^
| | | | c[3] = c[1] ^ c[2] ^ c[3]
| | | |
| | | c[5] = a[3] ^ a[4] ^ a[5]
| | |
| | c[8] is the result of a[1] ^ a[6] ^ a[7] ^ a[8]
| |
| c[17] = a[7] ^ a[10]
|
c[20] = a[10]
We have two 12-bit operands with the potential of making a 22-bit product. Each of the result bits will depend on some subset of bits of a masked by the bits of b. Each line of left-shifted a is marked with which set bit of b is responsible for its involvement within the summation. Result-bits of c are marked with which bit of a is involved in its summation. Here we can try to derive a pattern.
- Bit-
b[0]tells us if we should xor bit-a[i - 0]to result bit-c[i] - Bit-
b[1]tells us if we should xor bit-a[i - 1]to result bit-c[i] - Bit-
b[2]tells us if we should xor bit-a[i - 2]to result bit-c[i] - Bit-
b[j]tells us if we should xor bit-a[i - j]to result bit-c[i]
A concise and formal reduction of this multiplication can be induced:
In GF(2n), a polynomial multiplication of bits a and bits b into the result-bits c, looks like this:
$$c_i=\bigoplus_{j=0}^i a_jb_{i-j}$$
“The i-th result bit of
cis the summation(xor) of all the bits up to biti(inclusive) ofamultiplied(and) with the bits ofbup toi(inclusive) in reverse order.”
I might have done a bad job at explaining all of this, but there possibly better explanations out there.
Check out A PAINLESS GUIDE TO CRC ERROR DETECTION ALGORITHMS by Ross N. Williams for an even better introduction into the world of polynomial arithmetic in relation to CRC checksums.
Prefix Xor
What if a/b is all 1 bits(0xFFFFFFFFFFFFF.....)?
If all bits of b are going to be a 1, then the formal bit-definition looks more like this
$$c_i=\bigoplus_{j=0}^i a_j1=\bigoplus_{j=0}^i a_j$$
“The i-th result bit
cis the summation(xor) of the i-th bit ofaand all the bits before it”
This is a prefix xor operation! Also known as a cumulative scan or inclusive scan and can be summarized as:
c[0] = a[0]
c[1] = a[0] ^ a[1]
c[2] = a[0] ^ a[1] ^ a[2]
c[3] = a[0] ^ a[1] ^ a[2] ^ a[3]
c[4] = a[0] ^ a[1] ^ a[2] ^ a[3] ^ a[4]
...
Here’s what a prefix-xor looks like on varying input. Note how the hilighted bit changes the output below it.
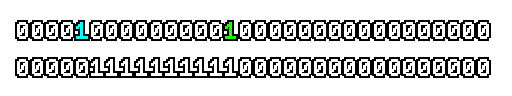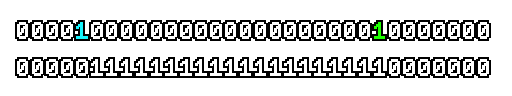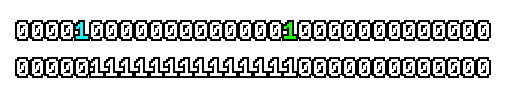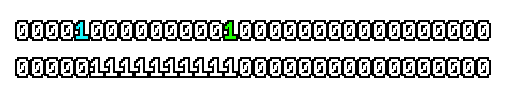
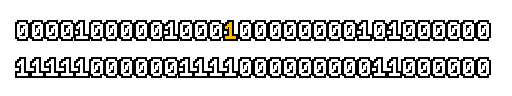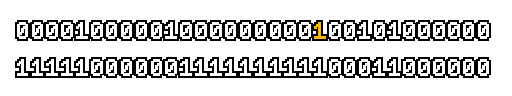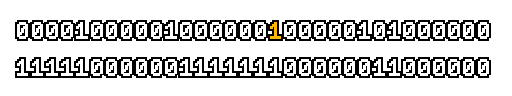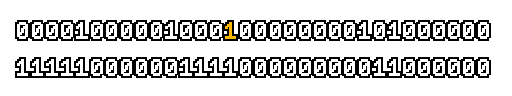
With this, you may “scan” the bits of an integer such that each bit is equal to the parity of itself and all the bits before it.
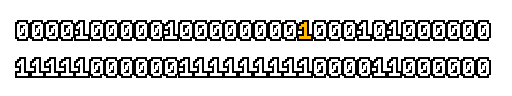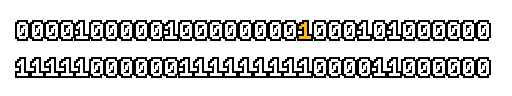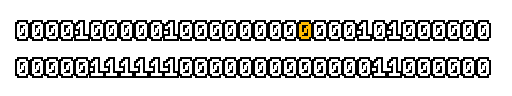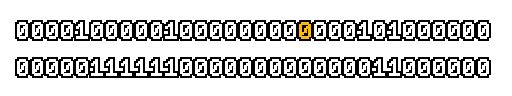
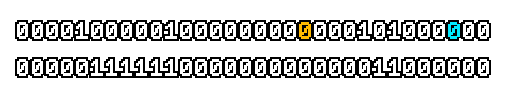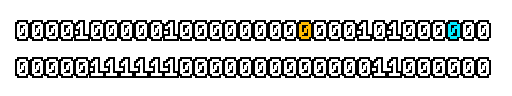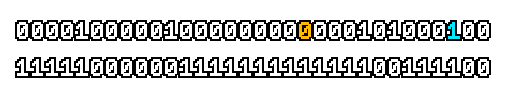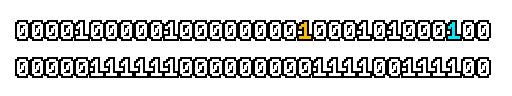
Big credits to Geoff Langdale for first documenting this great trick!
Bit Spread
What if a and b are both the same?
Lets map it out with some guided hand-arithemtic.
Without going into mathematical proofs, to keep things general, and map out the behavior of what would generally happen to any polynomial that we do this to, lets say I have some arbitrary polynomial:
xa + xb + xc + xd
If I did a general polynomial multiplication of this polynomial by itself, I get this result:
(xa + xb + xc + xd)(xa + xb + xc + xd) =
2xa + b + 2xa + c + 2xa + d + x2a + 2xb + c + 2xb + d + x2b + 2 xc + d + x2c + x2d
Then, if I was to mod-2 all the coefficients to put it back into a GF(2n) polynomial, I end up with this as a result:
All the terms with a 2 in front of it will get removed(2 % 2 = 0).
x2a + x2b + x2c + x2d
So we went from a, b, c, d to 2a, 2b, 2c, 2d!
In terms of bits, this would mean that each set bit in the binary-polynomial will be moved to the bit-index twice as far down(each bit-index i will now be at 2i). The set bit at a will now be at 2a, the bit set at b will now be at 2b, and so on. This can be described as a bit spread that can be used to accelerate bit interleaving. It will basically insert and interleave a 0 bit in-between each of the bits of the input polynomial.
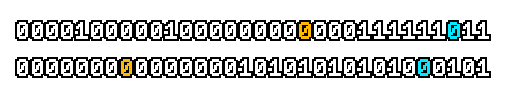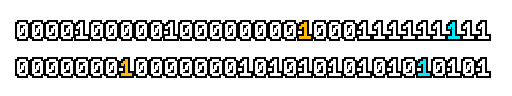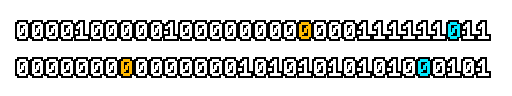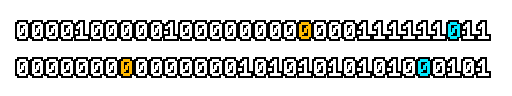
0000000000000001111111111111 –> 0001010101010101010101010101
0000000011000000 –> 0101000000000000
0000000000000011000000 —> 0000000101000000000000
This can be a very useful operation to accelerate the calculation of Morton codes and for Geohashing to map complex higher-dimensional values into a 1-dimensional index while preserving locality(increasing values are generally next to each other in their higher dimension).
x86/x64(pclmulqdq)
PCLMULQDQ is an elusive x86/x64 instruction that has other uses outside of its probably intended use.
CLMUL is an x86/x64 ISA extension that exposes polynomial carry-less multiplication.
CLMUL was introduced in Intel processors since Westmere(2010) and since AMD’s Jaguar(2013) processors. Any x86/x64 computer from the past 7 or so years will likely feature this extension.
pclmulqdq allows for a carry-less product of two 64-bit values into a destination 128-bit register. An additionally provided 2-bit integer determines which of the upper and lower 64-bit halfs of the the input xmm registers that will be multiplied together.
This intrinsic is exposed through the immintrin.h header and the _mm_clmulepi64_si128 instrinsic, taking two __m128i vector-registers and an integer value to select which upper/lower 64-bit lanes to multiply. Just the 0x00 selector will be fine for us(the lower 64-bits of each 128-bit register).
| Prototype | Operation |
|---|---|
_mm_clmulepi64_si128(xmm2, xmm1, 0x00) |
xmm2[ 63: 0] • xmm1[ 63: 0] |
_mm_clmulepi64_si128(xmm2, xmm1, 0x01) |
xmm2[ 63: 0] • xmm1[127:64] |
_mm_clmulepi64_si128(xmm2, xmm1, 0x10) |
xmm2[127:64] • xmm1[ 63: 0] |
_mm_clmulepi64_si128(xmm2, xmm1, 0x11) |
xmm2[127:64] • xmm1[127:64] |
pclmulqdq is defined exactly like our previously defined derivation.
IF (imm8[0] == 0)
TEMP1 := a[63:0]
ELSE
TEMP1 := a[127:64]
FI
IF (imm8[4] == 0)
TEMP2 := b[63:0]
ELSE
TEMP2 := b[127:64]
FI
FOR i := 0 to 63
TEMP[i] := (TEMP1[0] and TEMP2[i])
FOR j := 1 to i
TEMP[i] := TEMP[i] XOR (TEMP1[j] AND TEMP2[i-j])
ENDFOR
dst[i] := TEMP[i]
ENDFOR
FOR i := 64 to 127
TEMP[i] := 0
FOR j := (i - 63) to 63
TEMP[i] := TEMP[i] XOR (TEMP1[j] AND TEMP2[i-j])
ENDFOR
dst[i] := TEMP[i]
ENDFOR
dst[127] := 0
The first part looks familiar, but the second one looks like it iterates the bits backwards:
$$c_i=\bigoplus_{j=0}^i a_jb_{i-j} : 0 \leq i \leq n-1 $$
$$c_i=\bigoplus_{j=i-n+1}^{n-1} a_jb_{i-j} : n \leq i \leq 2n-2 $$
With n = 64 in the case of pclmulqdq:
$$c_i=\bigoplus_{j=0}^i a_jb_{i-j} : 0 \leq i \leq 63 $$
$$c_i=\bigoplus_{j=(i-64)+1}^{63} a_jb_{i-j} : 64 \leq i \leq 126 $$
Why is the result writing to a 128-bit register, but the definition of the result only defining bits
[0, 126]?Mentioned previously, the highest degree polynomial term that can be represented within a 32-bit integer is x31, so the highest degree polynomial that can result in multiplying two 32-bit polynomials is x62(x31 * x31 = x31 + 31 = x62)
So similarly, the highest degree polynomial term that can be represented with a 64-bit integer is x63, so the highest degree polynomial that can result in multiplying two 64-bit polynomials is x126(x63 * x63 = x63 + 63 = x126)
Prefix Xor
If we wanted to do a prefix-xor by setting b to all 1s, then the implementation would look like this.
$$c_i=\bigoplus_{j=0}^i a_j : 0 \leq i \leq 63 $$
$$c_i=\bigoplus_{j=(i-64)+1}^{63} a_j : 64 \leq i \leq 126 $$
Which would mean that the lower 64 bits is the prefix-xor as we would expect. While the upper 64 bits would be a prefix-xor from the opposite direction.
#include <cstdint>
#include <cstdio>
#include <bitset>
#include <immintrin.h>
int main()
{
const std::uint64_t Bits
= 0b00011000100000000001000000000010000000001000000100000001000000001;
// Print input value in binary
std::puts(("Bits:\t"+std::bitset<64>(Bits).to_string()).c_str());
const __m128i Result = _mm_clmulepi64_si128(
_mm_set_epi64x(0, Bits), // Input 64-bit "a"
_mm_set1_epi8(0xFF), // Input 128-bit "b'(full of 1 bits)
0 // Multiply the lower 64-bits of each of the inputs
);
const std::uint64_t Lo = _mm_cvtsi128_si64(Result); // Extract low 64-bits of result
const std::uint64_t Hi = _mm_extract_epi64(Result,1); // Extract high 64-bits of result
// Print result in binary
std::puts(("Lo:\t"+std::bitset<64>(Lo).to_string()).c_str());
std::puts(("Hi:\t"+std::bitset<64>(Hi).to_string()).c_str());
}
// Bits: 0011000100000000001000000000010000000001000000100000001000000001
// Lo: 1110111100000000000111111111110000000000111111100000000111111111
// Hi: 0001000011111111111000000000001111111111000000011111111000000000
You may curiously notice that while the
Hi64-bit result is a bitscan from the opposite direction, this is also just looks like a bit-inversion(~in C and C++) of theLoresult. This is not going to always be the case, and instead says something about the parity of your input bits.The original input value
Bitshas9bits set to1. If you were to go from left-to-right or right-to-left and flip a light switch every time you ran into a1-bit, you will always be left off in an opposite state than you started. If the original input value had8bits set to1and flipped a light switch each time you saw a1bit, then you would always end up in the same state that you started at. Geoff Langdale used this property in particular to quickly detect pairs of quote-characters.
Here are some other inputs and outputs, before you go thinking the Hi result is just a simple bit-inversion or copy of the Lo result.
Bits: 0011000100000000000000000000010000000001000000100000001000000001
Lo: 0001000011111111111111111111110000000000111111100000000111111111
Hi: 0001000011111111111111111111110000000000111111100000000111111111
Bits: 0011000100000000000000000000000000000000000000100000001000000001
Lo: 0001000011111111111111111111111111111111111111100000000111111111
Hi: 0001000011111111111111111111111111111111111111100000000111111111
Bits: 0000000000000000000000000000000000000000000000000000000000000001
Lo: 1111111111111111111111111111111111111111111111111111111111111111
Hi: 0000000000000000000000000000000000000000000000000000000000000000
Bits: 1000000000000000000000000000000000000000000000000000000000000000
Lo: 1000000000000000000000000000000000000000000000000000000000000000
Hi: 0111111111111111111111111111111111111111111111111111111111111111
Bits: 0000000000000000000000000001000000000000000000000000000000000000
Lo: 1111111111111111111111111111000000000000000000000000000000000000
Hi: 0000000000000000000000000000111111111111111111111111111111111111
Bits: 1111111111111111111111111111111111111111111111111111111111111111
Lo: 0101010101010101010101010101010101010101010101010101010101010101
Hi: 0101010101010101010101010101010101010101010101010101010101010101
Bits: 1111000011110000111100001111000011110000111100001111000011110000
Lo: 0101000001010000010100000101000001010000010100000101000001010000
Hi: 0101000001010000010100000101000001010000010100000101000001010000
And as a bonus, here are another couple tricks that can be derived from this too.
- BMO: Creates a bit-mask where every odd set bit from right-to-left bit is set to
1 - BSOP: Bit-Scans of all Odd-Parity areas
- Creates a mask between pairs of set
1bits, excluding the1bit itself. - Ex:
01000010->00111100
- Creates a mask between pairs of set
#include <cstdint>
#include <cstdio>
#include <bitset>
#include <immintrin.h>
int main()
{
const std::uint64_t Bits
= 0b0000000000010000000010000000100000001000000000000010000000000000;
// Print input value in binary
std::puts(("Bits:\t"+std::bitset<64>(Bits).to_string()).c_str());
const __m128i Result = _mm_clmulepi64_si128(
_mm_set_epi64x(0, Bits), // Input 64-bit "a"
_mm_set1_epi8(0xFF), // Input 128-bit "b'(full of 1 bits)
0 // Multiply the lower 64-bits of each of the inputs
);
const std::uint64_t Lo = _mm_cvtsi128_si64(Result); // Extract low 64-bits of result
const std::uint64_t Hi = _mm_extract_epi64(Result,1); // Extract high 64-bits of result
// Print result in binary
std::puts(("Lo:\t"+std::bitset<64>(Lo).to_string()).c_str());
std::puts(("Hi:\t"+std::bitset<64>(Hi).to_string()).c_str());
// Bit mask odds(mask odd set bits)
std::puts(("BMO:\t"+std::bitset<64>(Lo & Bits).to_string()).c_str());
// Bit scan odd parity ranges(exclusive)
std::puts(("BSOP:\t"+std::bitset<64>((~Bits) & Lo).to_string()).c_str());
}
// Bits: 0000000000010000000010000000100000001000000000000010000000000000
// Lo: 1111111111110000000001111111100000000111111111111110000000000000
// Hi: 0000000000001111111110000000011111111000000000000001111111111111
// BMO: 0000000000010000000000000000100000000000000000000010000000000000
// BSOP: 1111111111100000000001111111000000000111111111111100000000000000
Aug 29 2020:
Zach Wegner also points out that BMO can simply be implemented as
cmul(x, -2) & xas well.
Bit Spread
The bit-spread effect described earlier is as simple as multiplying the input value by itself! With the bonus that pclmulqdq gives us a 128 bit result too! So a full 64-bit value can be bit-spread into a 128-bit result, rather than just clipping the lower 64-bits(which would have ultimately limited the bit-spread to the lower 32-bits of a 64-bit input).
#include <cstdint>
#include <cstdio>
#include <bitset>
#include <immintrin.h>
int main()
{
const std::uint64_t Bits
= 0b0000000000000000000000000000000000000000000000000001111111111111;
// Print input value in binary
std::puts(("Bits:\t"+std::bitset<64>(Bits).to_string()).c_str());
const __m128i Result = _mm_clmulepi64_si128(
_mm_set_epi64x(0, Bits), // Input 64-bit "a"
_mm_set_epi64x(0, Bits), // Input 64-bit "a"
0 // Multiply the lower 64-bits of each of the inputs
);
const std::uint64_t Lo = _mm_cvtsi128_si64(Result); // Extract low 64-bits of result
const std::uint64_t Hi = _mm_extract_epi64(Result,1); // Extract high 64-bits of result
// Print result in binary
std::puts(("Lo:\t"+std::bitset<64>(Lo).to_string()).c_str());
std::puts(("Hi:\t"+std::bitset<64>(Hi).to_string()).c_str());
}
// Bits: 0000000000000000000000000000000000000000000000000001111111111111
// Lo: 0000000000000000000000000000000000000001010101010101010101010101
// Hi: 0000000000000000000000000000000000000000000000000000000000000000
// Some other sample inputs
// Bits: 0000000000000000000000000000000000001111111100000000000000000000
// Lo: 0000000001010101010101010000000000000000000000000000000000000000
// Hi: 0000000000000000000000000000000000000000000000000000000000000000
// Bits: 0000000001111111100000001111100000000000000000000000000000000000
// Lo: 0000000000000000000000000000000000000000000000000000000000000000
// Hi: 0000000000000000000101010101010101000000000000000101010101000000
// Bits: 0000000000000000000000000000000000000000000000000000000011000000
// Lo: 0000000000000000000000000000000000000000000000000101000000000000
// Hi: 0000000000000000000000000000000000000000000000000000000000000000
ARM(pmull/pmull2)
ARM is getting a brighter and brighter spotlight these days. Polynomials are a first-class resident in the AARCH64 ISA, as opposed to an x86 after-thought.
ARM provides the types poly16_t, poly64_t, and even poly128_t types through their arm_neon.h header. The pclmulqdq-equivalent would be the vmull_p64 intrinsic, which emits a pmull/pmull2 instruction that executes a polynomial multiplication of two 64-bit binary polynomials into a 128-bit result. pmull will multiply the low 64-bits of the input 128-bit registers., while pmull2 will multiply the upper 64-bits instead. This is similar to how pclmulqdq lets you elect which 64-bit lanes get multiplied.
pmull support is not indicated by baseline armv8 by default, and has to be tested for.
Or detected using the pmull flag in /proc/cpuinfo.
A minimal example:
#include <cstdint>
#include <cstdio>
#include <bitset>
#include <arm_neon.h>
int main()
{
const poly64_t Bits
= 0b00011000100000000001000000000010000000001000000100000001000000001;
// Print input value in binary
std::puts(("Bits:\t"+std::bitset<64>(Bits).to_string()).c_str());
const poly128_t Result = vmull_p64(
Bits, // Input 64-bit "a"
poly64_t(~0x0ul) // Input 128-bit "b'(full of 1 bits)
);
const std::uint64_t Lo = Result; // Extract low 64-bits of result
// Print result in binary
std::puts(("Lo:\t"+std::bitset<64>(Lo).to_string()).c_str());
}

