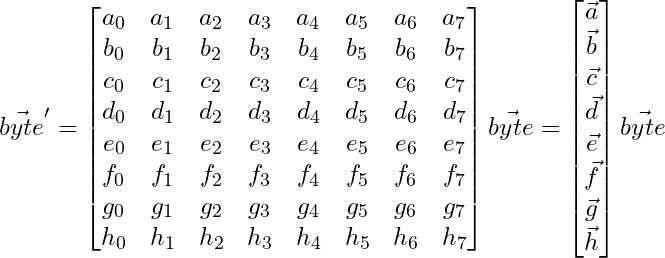
gf2p8affineqb is the latest and one of the longest-named instructions of the x86 ISA, featured in the GFNI extension(but is pretty much paired with AVX512VL as well).
At the moment, this instruction is only available in Sunny Cove(Icelake) based Intel architectures or newer by detecting CPUID (EAX=7,ECX=0):ECX[bit 08] or checking for the gfni flag in your /proc/cpuinfo.
Synopsis
__m128i _mm_gf2p8affine_epi64_epi8 (__m128i x, __m128i A, int b)
#include <immintrin.h>Instruction:
vgf2p8affineqb xmm, xmm, xmm, imm8CPUID Flags:
GFNI + AVX512VLDescription
Compute an affine transformation in the Galois Field 2^8. An affine transformation is defined by A * x + b, where A represents an 8 by 8 bit matrix, x > represents an 8-bit vector, and b is a constant immediate byte. Store the packed 8-bit results in dst.
Operation
DEFINE parity(x) { t := 0 FOR i := 0 to 7 t := t XOR x.bit[i] ENDFOR RETURN t } DEFINE affine_byte(tsrc2qw, src1byte, imm8) { FOR i := 0 to 7 retbyte.bit[i] := parity(tsrc2qw.byte[7-i] AND src1byte) XOR imm8.bit[i] ENDFOR RETURN retbyte } FOR j := 0 TO 1 FOR i := 0 to 7 dst.qword[j].byte[i] := affine_byte(A.qword[j], x.qword[j].byte[i], b) ENDFOR ENDFOR dst[MAX:128] := 0Performance
Architecture Latency Throughput (CPI) Icelake - 0.5
Intel Intrinsics guide, as of 2020-09-04
The AFFINEB instruction computes an affine transformation in the Galois Field 28. For this instruction, an affine transformation is defined by A * x + b where “A” is an 8 by 8 bit matrix, and “x” and “b” are 8-bit vectors. One SIMD register (operand 1) holds “x” as either 16, 32 or 64 8-bit vectors. A second SIMD (operand 2) register or memory operand contains 2, 4, or 8 “A” values, which are operated upon by the correspondingly aligned 8 “x” values in the first register. The “b” vector is constant for all calculations and contained in the immediate byte.
Intel Instruction manual, Vol. 2A 3-445
4343 AVX_GFNI :VGF2P8AFFINEQB xmm, xmm, xmm, imm8 L: 2.28ns= 3.0c T: 0.39ns= 0.50c
4344 AVX_GFNI :VGF2P8AFFINEQB ymm, ymm, ymm, imm8 L: 2.28ns= 3.0c T: 0.38ns= 0.50c
4345 AVX512VL_GFNI :{EVEX} VGF2P8AFFINEQB xm, xm, xm, im8 L: 2.28ns= 3.0c T: 0.39ns= 0.50c
4346 AVX512VL_GFNI :{EVEX} VGF2P8AFFINEQB ym, ym, ym, im8 L: 2.28ns= 3.0c T: 0.38ns= 0.50c
4347 AVX512F_GFNI :VGF2P8AFFINEQB zmm, zmm, zmm, imm8 L: 2.28ns= 3.0c T: 0.78ns= 1.02c
Icelake latency information, InstLatx64
Like pclmulqdq, vgf2p8affineqb was probably intended for finite field cryptography stuff but has other cool unintended benefits.
To put it simply, vgf2p8affineqb will do an 8x8 binary-matrix-transformation to each 8-bit byte of the input register and then add(GF(2) arithmetic, so a xor) to the resulting value.
The 8x8 binary-matrix is defined by a 64-bit value that gets applied to 8 respective bytes, and the value that gets xored after this transformation is provided as an 8-bit immediate value to the instruction.
In typical matrix fashion, each of the rows of the matrix determines how the resulting bits of the new 8-bit integer is defined. The bytes are defined in reverse order though, as the definition of the function defines its byte-indexing in reverse(
7 - i) order. Byte 0 defines how bit-7 is built, byte 1 defines how bit-6 is built, byte 2 defines how bit-5 is built, and so on.
You can think of it as a classic affine matrix-operation where each byte is treated as a boolean-vector within $\mathbb{R}^8$ that is transformed by an 8x8 matrix.
I’ll ignore the xor step by implying that the operand is is 0, the real interesting bit right now is the matrix transformation.
Similar to the actual definition of an affine transformation, we can now arbitrary do basically anything we want to the bits of each byte.
Now you can rotate, reverse, permute, shift, swizzle, etc. Anything a matrix can do.
For a 128-bit xmm register, two 64-bit bit-matrices will transform the 8 associated bytes that they overlap with in another xmm register.
Bit-reversal
For the opening trick, we’ll be reversing all 128-bits of an xmm register in two very fast and simple steps. First we reverse the bits in each byte, then we reverse the bytes of the entire register. This same principle would work with 256-bit registers, and 512-bit registers.
I’ll let the code speak for itself here.
#include <cstdint>
#include <cstddef>
#include <cstdio>
#include <bitset>
#include <immintrin.h>
// g++ -march=icelake-client
// Requires SSSE3 for `pshufb` and GFNI(+AVX512VL) for `vgf2p8affineqb`
__m128i BitReverse( __m128i Input )
{
return _mm_shuffle_epi8( // Step 2: Reverse the order of the bytes themselves
_mm_gf2p8affine_epi64_epi8( // Step 1: Reverse each of the within each byte
Input,
_mm_set1_epi64x(
// The 8x8 binary-matrix, defined as a 64-bit value (8x8=64)
// I've broken up the binary values with "'" characters so that
// you may see the individual rows of the 8x8 matrix
// This is the same as:
// [ 1 0 0 0 0 0 0 0 ] < Byte 7, Bit 0
// [ 0 1 0 0 0 0 0 0 ] < Byte 6, Bit 1
// [ 0 0 1 0 0 0 0 0 ] < Byte 5, Bit 2
// X' = [ 0 0 0 1 0 0 0 0 ] < Byte 4, Bit 3 * X + 0
// [ 0 0 0 0 1 0 0 0 ] < Byte 3, Bit 4
// [ 0 0 0 0 0 1 0 0 ] < Byte 2, Bit 5
// [ 0 0 0 0 0 0 1 0 ] < Byte 1, Bit 6
// [ 0 0 0 0 0 0 0 1 ] < Byte 0, Bit 7
0b10000000'01000000'00100000'00010000'00001000'00000100'00000010'00000001
),
0 // We don't care to do a final `xor` to the result, so keep this 0
),
_mm_set_epi8(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15) // Reverse byte-indices
);
}
void Print( __m128i Input )
{
std::printf(
"%.64s%.64s\n",
std::bitset<64>(_mm_cvtsi128_si64(Input )).to_string().c_str(),
std::bitset<64>(_mm_extract_epi64(Input,1)).to_string().c_str()
);
}
int main()
{
__m128i TestVec = _mm_set_epi64x(0xBEEFBEEFBEEFBEEFull,0xDEADDEADDEADDEADull);
Print(TestVec);
Print(BitReverse(TestVec));
}
// Output:
// 11011110101011011101111010101101110111101010110111011110101011011011111011101111101111101110111110111110111011111011111011101111
// 11110111011111011111011101111101111101110111110111110111011111011011010101111011101101010111101110110101011110111011010101111011
Is reversing huge byte-vectors useful though? Maybe not to most people.
I recently used this to reimplement ARM’s vector-bit-reversal instruction in yuzu’s ARM recompiler backend.
Any other method would have likely involved a pshufb-based look-up-table method
by using the upper and lower 4-bits of each byte, and or-ing them together.
With gf2p8affineqb, now its a much more concise and faster operation.
And gf2p8affineqb has plenty more tricks up its sleeve.

